A Set of Reading Scores for Fourth Grade Children Has a Mean of 25 and Standard Deviation of 5.

The Normal Distribution

xxx The Standard Normal Distribution

The standard normal distribution is a normal distribution of standardized values called z-scores. A z-score is measured in units of the standard divergence.

The mean for the standard normal distribution is zero, and the standard deviation is one. What this does is dramatically simplify the mathematical adding of probabilities. Take a moment and substitute zilch and one in the appropriate places in the in a higher place formula and you can run into that the equation collapses into one that can be much more easily solved using integral calculus. The transformation z = produces the distribution Z ~ North(0, 1). The value x in the given equation comes from a known normal distribution with known mean μ and known standard difference σ. The z-score tells how many standard deviations a particular x is abroad from the mean.

Z-Scores

If X is a ordinarily distributed random variable and Ten ~ North(μ, σ), then the z-score for a particular x is:

The z-score tells you lot how many standard deviations the value x is above (to the right of) or below (to the left of) the mean, μ. Values of x that are larger than the mean take positive z-scores, and values of x that are smaller than the hateful accept negative z-scores. If x equals the mean, and so ten has a z-score of zip.

Suppose X ~ N(five, 6). This says that Ten is a usually distributed random variable with mean μ = 5 and standard deviation σ = 6. Suppose ten = 17. So:

This means that x = 17 is two standard deviations (2σ) above or to the correct of the mean μ = 5.

At present suppose x = 1. Then: z = = = –0.67 (rounded to two decimal places)

This means that 10 = one is 0.67 standard deviations (–0.67σ) below or to the left of the mean μ = 5.

The Empirical DominionIf X is a random variable and has a normal distribution with hateful µ and standard deviation σ, then the Empirical Rule states the following:

• Virtually 68% of the 10 values lie between –aneσ and +1σ of the mean µ (within i standard deviation of the mean).
• Almost 95% of the 10 values lie betwixt –2σ and +2σ of the mean µ (within two standard deviations of the mean).
• About 99.7% of the x values lie betwixt –3σ and +3σ of the mean µ (within three standard deviations of the mean). Notice that almost all the ten values lie within three standard deviations of the mean.
• The z-scores for +oneσ and –1σ are +1 and –1, respectively.
• The z-scores for +2σ and –twoσ are +2 and –ii, respectively.
• The z-scores for +3σ and –3σ are +iii and –3 respectively.

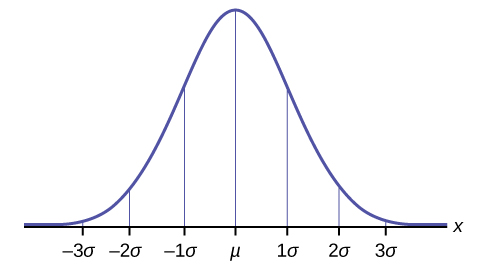
Suppose x has a normal distribution with hateful 50 and standard departure 6.

• Most 68% of the x values lie within 1 standard difference of the mean. Therefore, about 68% of the x values lie between –1σ = (–1)(half dozen) = –6 and 1σ = (i)(vi) = 6 of the hateful 50. The values 50 – vi = 44 and 50 + 6 = 56 are within one standard deviation from the mean l. The z-scores are –1 and +ane for 44 and 56, respectively.
• Nigh 95% of the 10 values lie inside two standard deviations of the mean. Therefore, most 95% of the 10 values prevarication betwixt –2σ = (–two)(6) = –12 and 2σ = (2)(6) = 12. The values 50 – 12 = 38 and fifty + 12 = 62 are within two standard deviations from the mean 50. The z-scores are –two and +2 for 38 and 62, respectively.
• Near 99.seven% of the x values prevarication inside three standard deviations of the mean. Therefore, about 95% of the 10 values lie between –3σ = (–iii)(half-dozen) = –xviii and 3σ = (3)(six) = eighteen of the mean 50. The values 50 – 18 = 32 and fifty + 18 = 68 are within three standard deviations from the hateful l. The z-scores are –3 and +3 for 32 and 68, respectively.

Chapter Review

A z-score is a standardized value. Its distribution is the standard normal, Z ~ North(0, 1). The mean of the z-scores is zero and the standard deviation is 1. If z is the z-score for a value ten from the normal distribution Due north(µ, σ) and so z tells you how many standard deviations x is above (greater than) or below (less than) µ.

Formula Review

Z ~ N(0, 1)

z = a standardized value (z-score)

hateful = 0; standard deviation = 1

To find the k ^th percentile of X when the z-scores is known:
k = μ + (z)σ

z-score: z = or z =

Z = the random variable for z-scores

Z ~ Due north(0, ane)

A canteen of water contains 12.05 fluid ounces with a standard deviation of 0.01 ounces. Ascertain the random variable X in words. 10 = ____________.

ounces of water in a bottle

A normal distribution has a mean of 61 and a standard deviation of 15. What is the median?

<!– <solution id="fs-idm63161360″> 61 –>

A company manufactures rubber balls. The mean diameter of a ball is 12 cm with a standard deviation of 0.2 cm. Define the random variable Ten in words. X = ______________.

<!– <solution id="fs-idp15866016″> diameter of a rubber ball –>

X ~ N(–4, i)

What is the median?

–four

<!– <solution id="fs-idm120454704″> 5 –>

What does a z-score measure out?

<!– <solution id="fs-idm57247936″> The number of standard deviations a value is from the hateful. –>

What does standardizing a normal distribution exercise to the mean?

The mean becomes zero.

Is X ~ North(0, 1) a standardized normal distribution? Why or why not?

<!– <solution id="fs-idp48272224″> Yeah because the mean is zero, and the standard deviation is one. –>

What is the z-score of x = 12, if it is 2 standard deviations to the right of the hateful?

z = 2

What is the z-score of 10 = 9, if it is 1.5 standard deviations to the left of the hateful?

<!– <solution id="fs-idp6573504″> z = –1.5 –>

What is the z-score of ten = –2, if it is 2.78 standard deviations to the right of the hateful?

z = 2.78

What is the z-score of x = seven, if information technology is 0.133 standard deviations to the left of the hateful?

<!– <solution id="fs-idp38051616″> z = –0.133 –>

Suppose Ten ~ N(2, 6). What value of x has a z-score of three?

ten = 20

Suppose 10 ~ Due north(viii, i). What value of x has a z-score of –2.25?

<!– <solution id="fs-idp19875360″> 10 = 5.75 –>

Suppose 10 ~ N(9, five). What value of x has a z-score of –0.v?

x = vi.v

Suppose X ~ North(two, iii). What value of x has a z-score of –0.67?

<!– <solution id="fs-idp31923120″> x = –0.01 –>

Suppose X ~ N(four, 2). What value of x is i.5 standard deviations to the left of the mean?

ten = i

Suppose X ~ N(4, 2). What value of x is two standard deviations to the right of the hateful?

<!– <solution id="fs-idm47755696″> 10 = 8 –>

Suppose X ~ N(8, 9). What value of ten is 0.67 standard deviations to the left of the mean?

x = 1.97

Suppose Ten ~ N(–1, 2). What is the z-score of x = 2?

<!– <solution id="fs-idm119642576″> z = 1.5 –>

Suppose X ~ North(12, half-dozen). What is the z-score of 10 = 2?

z = –one.67

Suppose X ~ N(nine, 3). What is the z-score of x = nine?

<!– <solution id="fs-idm56843792″> z = 0 –>

Suppose a normal distribution has a hateful of six and a standard deviation of ane.5. What is the z-score of x = 5.5?

z ≈ –0.33

In a normal distribution, ten = 5 and z = –1.25. This tells you that x = five is ____ standard deviations to the ____ (correct or left) of the mean.

<!– <solution id="fs-idm62539280″> 1.25, left –>

In a normal distribution, x = 3 and z = 0.67. This tells you lot that x = iii is ____ standard deviations to the ____ (right or left) of the mean.

0.67, right

In a normal distribution, x = –two and z = 6. This tells you lot that x = –2 is ____ standard deviations to the ____ (right or left) of the mean.

<!– <solution id="fs-idm102069296″> six, right –>

In a normal distribution, x = –5 and z = –three.14. This tells y'all that x = –five is ____ standard deviations to the ____ (right or left) of the mean.

3.14, left

In a normal distribution, x = six and z = –1.seven. This tells you that ten = 6 is ____ standard deviations to the ____ (correct or left) of the mean.

<!– <solution id="fs-idm98531584″> 1.7, left –>

About what percent of x values from a normal distribution lie within ane standard deviation (left and correct) of the mean of that distribution?

nearly 68%

About what percentage of the x values from a normal distribution prevarication within two standard deviations (left and right) of the hateful of that distribution?

<!– <solution id="fs-idm47813520″> about 95.45% –>

About what percentage of x values lie between the 2nd and third standard deviations (both sides)?

about 4%

Suppose X ~ Due north(xv, three). Between what ten values does 68.27% of the data lie? The range of x values is centered at the mean of the distribution (i.e., fifteen).

<!– <solution id="fs-idm33513040″> betwixt 12 and 18 –>

Suppose X ~ N(–3, 1). Between what x values does 95.45% of the data prevarication? The range of x values is centered at the mean of the distribution(i.e., –3).

betwixt –5 and –one

Suppose Ten ~ N(–3, 1). Between what ten values does 34.14% of the data prevarication?

<!– <solution id="fs-idm68579024″> betwixt –iv and –iii or between –three and –2 –>

Near what percent of ten values lie betwixt the hateful and three standard deviations?

near 50%

About what percent of x values lie between the mean and 1 standard difference?

<!– <solution id="fs-idp3556992″> nigh 34.14% –>

About what percent of x values prevarication betwixt the kickoff and second standard deviations from the mean (both sides)?

nigh 27%

Virtually what percent of 10 values lie betwween the first and third standard deviations(both sides)?

<!– <solution id="fs-idp56159920″> about 34.46% –>

Utilise the following information to answer the next ii exercises: The life of Sunshine CD players is usually distributed with mean of 4.ane years and a standard deviation of 1.3 years. A CD thespian is guaranteed for three years. We are interested in the length of time a CD player lasts.

Define the random variable X in words. Ten = _______________.

The lifetime of a Sunshine CD player measured in years.

X ~ _____(_____,_____)

<!– <solution id="fs-idp89883200″> X ~ N(4.1, 1.3) –>

Homework

Use the following information to reply the next 2 exercises: The patient recovery fourth dimension from a particular surgical procedure is usually distributed with a mean of v.3 days and a standard deviation of 2.ane days.

What is the median recovery time?

1. 2.7
2. 5.3
3. vii.4
4. two.1

<!– <solution id="fs-idm68359392″> b –>

What is the z-score for a patient who takes ten days to recover?

1. 1.5
2. 0.ii
3. two.2
4. 7.3

c

The length of time to find it takes to observe a parking space at ix A.Grand. follows a normal distribution with a mean of five minutes and a standard deviation of two minutes. If the mean is significantly greater than the standard divergence, which of the following statements is true?

1. The information cannot follow the uniform distribution.
2. The information cannot follow the exponential distribution..
3. The data cannot follow the normal distribution.

1. I only
2. Ii only
3. III simply
4. I, Ii, and 3

<!– <solution id="fs-idp16013392″> b –>

The heights of the 430 National Basketball Association players were listed on team rosters at the commencement of the 2005–2006 season. The heights of basketball players accept an approximate normal distribution with mean, µ = 79 inches and a standard deviation, σ = 3.89 inches. For each of the following heights, summate the z-score and translate information technology using complete sentences.

1. 77 inches
2. 85 inches
3. If an NBA player reported his elevation had a z-score of 3.5, would you believe him? Explain your answer.

1. Use the z-score formula. z = –0.5141. The tiptop of 77 inches is 0.5141 standard deviations beneath the mean. An NBA player whose height is 77 inches is shorter than average.
2. Utilize the z-score formula. z = i.5424. The height 85 inches is 1.5424 standard deviations above the mean. An NBA player whose height is 85 inches is taller than boilerplate.
3. Height = 79 + 3.v(iii.89) = 92.615 inches, which is taller than vii feet, 8 inches. There are very few NBA players this tall then the respond is no, not likely.

The systolic blood pressure (given in millimeters) of males has an approximately normal distribution with mean µ = 125 and standard deviation σ = 14. Systolic blood pressure for males follows a normal distribution.

1. Summate the z-scores for the male systolic blood pressures 100 and 150 millimeters.
2. If a male friend of yours said he idea his systolic blood pressure was ii.5 standard deviations beneath the mean, merely that he believed his blood pressure level was between 100 and 150 millimeters, what would you say to him?

<!– <solution id="eip-774″> Use the z-score formula. 100 – 125 14 ≈ –1.eight and 100 – 125 14 ≈ 1.8 I would tell him that 2.v standard deviations below the hateful would give him a blood pressure level reading of 90, which is below the range of 100 to 150. –>

Kyle'due south dr. told him that the z-score for his systolic blood pressure is 1.75. Which of the post-obit is the best interpretation of this standardized score? The systolic blood pressure level (given in millimeters) of males has an approximately normal distribution with hateful µ = 125 and standard deviation σ = 14. If X = a systolic blood pressure level score then 10 ~ North (125, 14).

1. Which answer(s) is/are correct?
   1. Kyle's systolic blood pressure is 175.
   2. Kyle's systolic blood pressure is 1.75 times the average blood pressure of men his historic period.
   3. Kyle'due south systolic blood pressure is ane.75 above the boilerplate systolic blood pressure of men his age.
   4. Kyles'due south systolic blood pressure level is 1.75 standard deviations in a higher place the boilerplate systolic blood pressure for men.
2. Summate Kyle'due south claret pressure level.

1. iv
2. Kyle'southward blood pressure is equal to 125 + (one.75)(14) = 149.5.

Peak and weight are two measurements used to track a kid's development. The World Health System measures child development by comparing the weights of children who are the same height and the same gender. In 2009, weights for all 80 cm girls in the reference population had a mean µ = ten.2 kg and standard divergence σ = 0.8 kg. Weights are unremarkably distributed. X ~ N(10.2, 0.8). Summate the z-scores that represent to the following weights and interpret them.

1. xi kg
2. 7.9 kg
3. 12.2 kg

<!– <solution id="eip-182″> 11 – 10.ii 0.viii = 1 A child who weighs 11 kg is 1 standard deviation above the mean of x.2 kg. vii.ix – 10.2 0.8 = –2.875 A kid who weighs seven.ix kg is 2.875 standard deviations below the mean of 10.2 kg. 12.2 – 10.2 0.8 = two.five A kid who weighs 12.2 kg is ii.5 standard deviation above the mean of 10.two kg. –>

In 2005, 1,475,623 students heading to college took the Sabbatum. The distribution of scores in the math department of the SAT follows a normal distribution with mean µ = 520 and standard deviation σ = 115.

1. Calculate the z-score for an Saturday score of 720. Translate it using a complete judgement.
2. What math SAT score is 1.five standard deviations above the hateful? What tin y'all say about this SAT score?
3. For 2012, the Saturday math test had a mean of 514 and standard divergence 117. The Act math test is an alternating to the Sabbatum and is approximately normally distributed with hateful 21 and standard deviation five.three. If one person took the SAT math test and scored 700 and a 2nd person took the Act math exam and scored 30, who did meliorate with respect to the test they took?

<!– <para id="fs-idp207361600″>Utilize the post-obit data to answer the next three exercises: X ~ U(iii, 13) –>

brettyoult1948.blogspot.com

Source: https://opentextbc.ca/introbusinessstatopenstax/chapter/the-standard-normal-distribution/

Share this post